Teoría de conjuntos.

Definición de conjuntos.

¿Qué es un conjunto?

Un conjunto es una colección de objetos sin orden que pueden ser números, letras, personas y sin repetición. . Por ejemplo 𝑨 = {𝟏, 𝟐, 𝟑, 𝟒, 𝟓}  ,   𝑩 = {𝒂, 𝒃, 𝒄, 𝒅, 𝒆}.

Un conjunto se denota encerrado entre llaves todos los elementos del conjunto si los elementos están expresados en forma de lista se dicen que el conjunto está expresado por extensión, por ejemplo: 

𝑨 = {2,3,4,5,6,7,8} 

𝑴 = {𝑡, 𝑖, 𝑔, 𝑟,𝑒} 

𝑵 = {𝑎,𝑒, 𝑖, 𝑜, 𝑢}

Si los elementos están expresados por una regla o característica de todos los elementos, se dice que el conjunto está expresado por comprensión, por ejemplo, 

1. {𝑥/ 𝑥 𝑒𝑠 𝑢𝑛 𝑛ú𝑚𝑒𝑟𝑜 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑜 𝑚𝑒𝑛𝑜𝑟 𝑞𝑢𝑒 6} 

2. {𝐿𝑎𝑠 𝑣𝑜𝑐𝑎𝑙𝑒𝑠} 

3. {𝐿𝑒𝑡𝑟𝑎𝑠 𝑑𝑒 𝑙𝑎 𝑝𝑎𝑙𝑎𝑏𝑟𝑎 "tigre"}

Para representar gráficamente un conjunto a menudo se utiliza un óvalo en cuyo interior se ubican todos los elementos del conjunto, esta representación se conoce como Diagrama de Venn.

¿Qué es un subconjunto? 

Se denomina subconjunto al conjunto que se encuentra dentro de otro conjunto, es decir, el conjunto B es subconjunto del conjunto A, si todos los elementos de B están incluidos en A. 

Por ejemplo: 

• Los mamíferos son un subconjunto del conjunto animales.
• Los números impares son un subconjunto del conjunto de números naturales. 
• El "conjunto de todas las mujeres" es un subconjunto del "conjunto de todas las personas"

Conjunto unitario: un conjunto unitario se distingue por tener solo un elemento. No importa qué tipo de elemento tenga el conjunto, un número, una letra o cualquier otra cosa, si tiene un solo elemento es llamado conjunto unitario.

Conjunto Vacio: Es aquel conjunto que no tiene elementos. Para representar dicho conjunto usamos el reconocido símbolo del vacío.

Conjunto Universal: un conjunto universal es un conjunto formado por todos los objetos de estudio en un contexto dado.

Conjunto disjuntos: Son aquellos que no tienen ningún elemento en común. Es decir, los conjuntos A y B son disjuntos si se cumple que su intersección es un conjunto vacío.

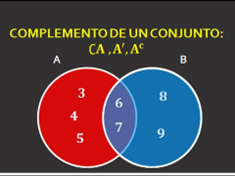
Complemento de conjuntos:  Es aquel que incluye todos los elementos que no están contenidos en dicho conjunto.

Cardinalidad de conjuntos: es la cantidad de elementos que tiene un conjunto dado.